关于信号相关知识的深入探究。

傅里叶变换

1. 为什么傅里叶变换能做时域 ⇄ 频域转换？

因为它基于这样一个假设（或者说事实）：

任意一个信号（只要满足一些条件）都可以看作是不同频率的正弦波和余弦波的叠加。

傅里叶变换就是一个投影运算：

• 把信号投影到一系列正弦/余弦（或复指数）“基底”上
• 得到的投影系数就是各个频率成分的强度和相位

它本质上和“分解向量到基底”是一个道理，只不过：

• 向量分解用的基是
• 信号分解用的基是

---

2. 举一个最简单的例子

假设我们有一个时域信号：

$$x(t) = \sin(2\pi \cdot 3 t)$$

单位是秒，采样率够高。它就是一个纯 3 Hz 的正弦波。

---

步骤 1 — 定义频率基底

我们假设信号可能包含从 0 Hz 到 10 Hz 的成分，每个成分都是：

$$e^{-j 2\pi f t}$$

（复指数等价于正弦+余弦）。

---

步骤 2 — 投影到每个频率

傅里叶变换公式：

$$X(f) = \int_{-\infty}^{+\infty} x(t) \cdot e^{-j 2\pi f t} \, dt$$

我们把 和 相乘后积分，这个积分结果就是在频率 上的权重。

---

步骤 3 — 得到频谱

• 当 Hz：
  和基底 完全同频同相，积分会得到一个很大的值（最大投影）。
• 当 Hz：
  积分会出现大量正负抵消（因为波峰波谷不对齐），结果接近 0。

所以我们会得到：

$$X(f) \ \text{在 } f=3 \text{处有一个尖峰，其它频率几乎为 0}$$

这就是频域信号——它告诉你：
“这个信号里只含有 3 Hz 的成分，幅度是多少，初相是多少。”

---

3. 背后的数学本质

傅里叶变换的本质是：

• 基底函数正交性：不同频率的正弦/余弦是正交的（积分内积为 0）。
• 变换就是内积/投影：用积分计算信号在每个基底方向的投影系数。
• 频域只是这些投影系数的集合。

类比：

• 时域：描述信号随时间变化的波形。
• 频域：描述信号由哪些“频率基底”组成，每个成分的大小与相位。

---

4. 蕴含的深层意义

• 时域是局部特征，频域是全局特征：
  一个正弦波在时域可能看起来只是震动，但在频域它是一个点。
• 能量守恒（帕塞瓦尔定理）：时域信号能量 = 频域信号能量。
• 线性变换：傅里叶变换是一个线性算子，叠加原理成立。
• 基底变换：其实就是从“时间基底”切换到“频率基底”。

5. 傅里叶变换的示例

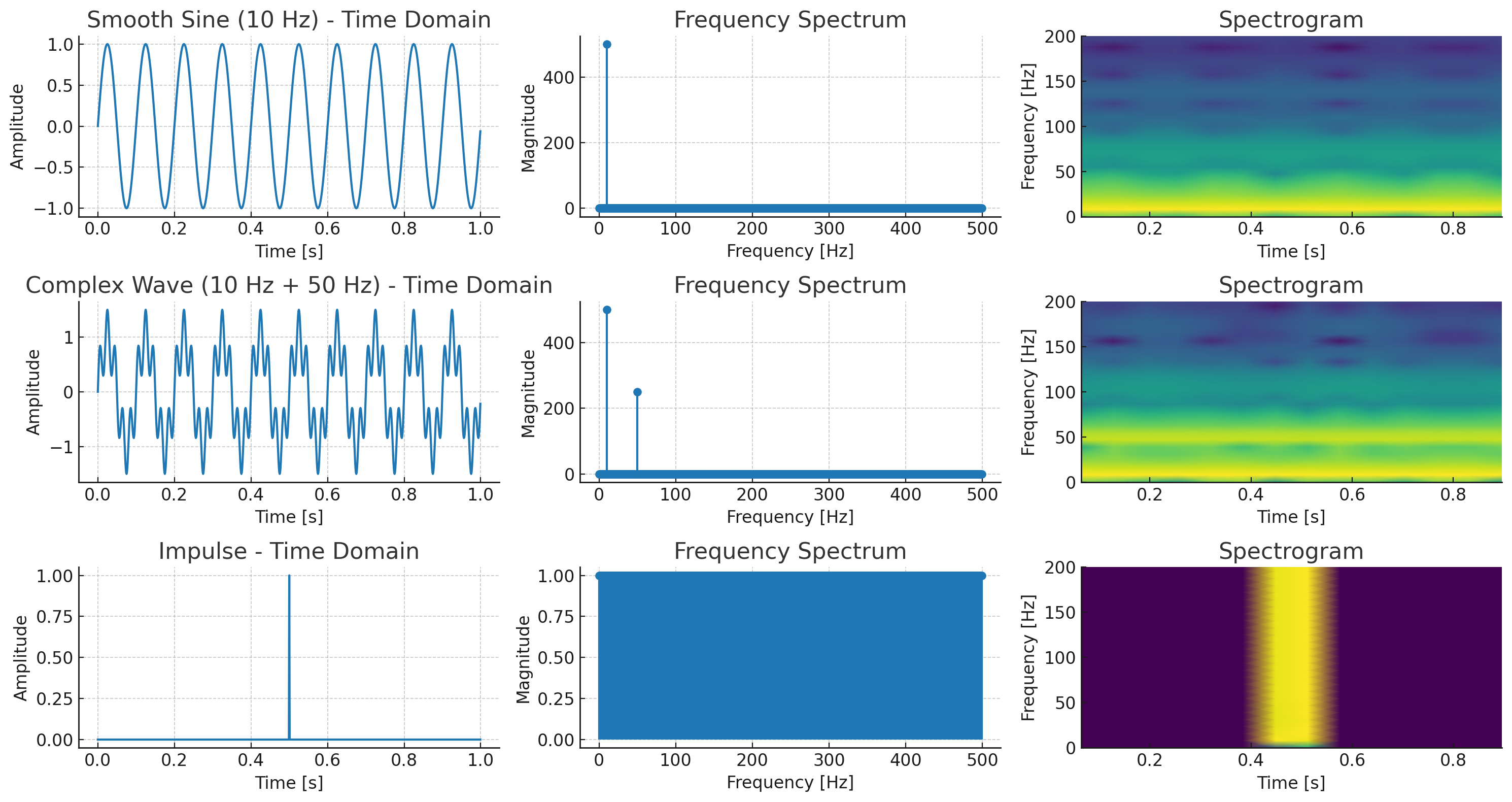
这里的三行展示了同一信号在三种视角下的表现：

1. 平滑正弦波（10 Hz）

   • 频谱：在 10 Hz 出现一个尖峰 → 窄带信号。
   • 声谱图：始终只在 10 Hz 附近有能量，随时间保持不变。

2. 稍复杂波形（10 Hz + 50 Hz）

   • 频谱：两个明显的尖峰 → 带宽比单频正弦更宽。
   • 声谱图：两个水平亮线（10 Hz 和 50 Hz），全程存在。

3. 脉冲

   • 频谱：几乎全频都有能量 → 宽带信号。
   • 声谱图：只有脉冲时刻出现全频亮起，之后消失。

这直观体现了带宽和时域变化的关系：变化越快（突变越强），频域分布越宽；变化越慢，频域越集中。