Hugo's Cyber Heritage

Shine or Die

Algorithm：Overall Review

发表于 更新于 分类于
本文字数： 282 阅读时长 ≈ 1 分钟

算法总复习，包含分治，图算法，动态规划，线性规划，P与NP，规约等重点知识的总结。

Divide and Conquer

Master theorem:

for some constants (a>0) , (b>1) ,and (d ≥0) , then

d代表非递归部分（即每次递归调用之外的操作）的时间复杂度的指数。

证明：分析递归树的总工作量

FFT

Graph Algorithms

DFS

1
2
3
4
5
6
7
8
9
10
11
12
13
14
EXPLORE(G, v):  
1. visited[v] = true  
2. pre[v] = clock; clock++      # 记录发现时间  
3. for each edge (v, u) ∈ E:  
4.    if not visited[u]:  
5.        EXPLORE(G, u)  
6. post[v] = clock; clock++     # 记录离开时间  

DFS(G):  
1. for all v ∈ V: visited[v] = false  
2. clock = 0  
3. for all v ∈ V:  
4.    if not visited[v]:  
5.        EXPLORE(G, v)

running time：O(|V|+|E|)

SCC （强连通分量）

1
2
3
4
5
6
7
8
9
10
11
12
13
Input: 有向图 G = (V, E)
Output: G 的强连通分量
1. DFS(G)  # 执行 DFS，记录每个节点的 post 时间
2. 按 post 时间降序排列 V
3. G' = G 的转置图 （将所有边反向）
4. visited = false for all v ∈ V
5. for each v in V (按 post 时间降序):
6.    if not visited[v]:
7.        SCC = {}  # 当前强连通分量
8.        EXPLORE(G', v)  # 在转置图上进行 DFS
9.        for each u in SCC:
10.           visited[u] = true  # 标记已访问
11.           print(u)  # 输出当前强连通分量的节点

running time：O(|V|+|E|)

Dijkstra

1
2
3
4
5
6
7
8
9
10
11
12
13
14
**Input**: 图 G, 边权 ℓ, 起点 s  
**Output**: 所有节点到 s 的最短距离 dist[]  

1. for each u ∈ V:  
2.    dist[u] = ∞; prev[u] = nil  
3. dist[s] = 0  
4. H = 优先队列 (key=dist)   # 初始包含所有节点  
5. while H 非空:  
6.    u = H.deletemin()     # 取出 dist 最小的节点  
7.    for each 边 (u, v) ∈ E:  
8.        if dist[v] > dist[u] + ℓ(u, v):  
9.            dist[v] = dist[u] + ℓ(u, v)  
10.           prev[v] = u  
11.           H.decreasekey(v)  # 更新 v 在队列中的优先级

Bellman-Ford

1
2
3
4
5
6
7
8
9
10
11
12
13
14
**Input**: 图 G, 边权 ℓ, 起点 s（无负环）  
**Output**: 最短距离 dist[]，或报告负环  

1. for each u ∈ V:  
2.    dist[u] = ∞; prev[u] = nil  
3. dist[s] = 0  
4. repeat |V| - 1 次:  
5.    for each 边 e = (u, v) ∈ E:  
6.        if dist[v] > dist[u] + ℓ(u, v):  
7.            dist[v] = dist[u] + ℓ(u, v)  
8.            prev[v] = u  
9. for each 边 e = (u, v) ∈ E:  
10.   if dist[v] > dist[u] + ℓ(u, v):  
11.       return "存在负环"

running time：O(|V| * |E|)

DAG 最短路

拓扑顺序是指在有向无环图（DAG）中，所有边 (u, v) 都满足 u 在 v 之前的线性序列。

1
2
3
4
5
6
7
8
9
10
11
12
Input: DAG G, 边权 ℓ, 起点 s  
Output: 最短距离 dist[]  

1. for each u ∈ V:  
2.    dist[u] = ∞; prev[u] = nil  
3. dist[s] = 0  
4. L = 拓扑排序(G)   # 按线性序排列节点  
5. for each u ∈ L (按序处理):  
6.    for each 边 (u, v) ∈ E:  
7.        if dist[v] > dist[u] + ℓ(u, v):  
8.            dist[v] = dist[u] + ℓ(u, v)  
9.            prev[v] = u

running time: O(|V| + |E|)

MST （最小生成树）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
Kruskal(G)
// Input: 无向图 G = (V, E)
// Output: 最小生成树 T
1. T = ∅  // 初始化最小生成树
2. for each edge (u, v) ∈ E in increasing order of weight:
3.    if u and v are in different components:
4.        T = T ∪ {(u, v)}  // 添加边到最小生成树
5.        union(u, v)  // 合并 u 和 v 的连通分量

Prim(G, s)
// Input: 无向图 G = (V, E), 起点 s
// Output: 最小生成树 T
1. T = ∅  // 初始化最小生成树
2. for each vertex v ∈ V: dist[v] = ∞; prev[v] = nil
3. dist[s] = 0  // 起点到自身的距离为 0
4. H = 优先队列 (key=dist)  // 初始化优先队列
5. while H 非空:
6.    u = H.deletemin()  // 取出距离最小的节点
7.    for each 边 (u, v) ∈ E:
8.        if dist[v] > ℓ(u, v):  // 如果找到更小的边
9.            dist[v] = ℓ(u, v)  // 更新距离
10.           prev[v] = u  // 更新前驱节点
11.           H.decreasekey(v)  // 更新优先队列中的优先级

切割性质：对于图G的任意切割(S, V-S)，连接S和V-S的最小权重边必然在某个MST中。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
并查集

# 初始化单元素集合  
makeset(x):  
1. π[x] = x      # 父指针  
2. rank[x] = 0   # 秩  

# 查找根（带路径压缩）  
find(x):  
1. if x ≠ π[x]:  
2.   π[x] = find(π[x])  # 递归压缩路径  
3. return π[x]  

# 合并集合（按秩合并）  
union(x,y):  
1. rx = find(x), ry = find(y)  
2. if rx == ry: return  
3. if rank[rx] > rank[ry]:  
4.   π[ry] = rx  
5. else:  
6.   π[rx] = ry  
7.   if rank[rx] == rank[ry]:  
8.     rank[ry]++

Dynamic Programming

动态规划（Dynamic Programming）

  • 核心思想：将问题分解为重叠子问题，存储子问题解避免重复计算。
  • 关键步骤：
    1. 定义子问题
    2. 建立递推关系（状态转移方程）
    3. 确定计算顺序（自底向上或记忆化搜索）
  • 应用场景：
    • 最长递增子序列 (LIS)：以 j 结尾的 LIS 长度
    • 编辑距离：字符串对齐的最小差异代价，
    • 背包问题：
      • 重复背包：
      • 01 背包：
    • 矩阵链乘法：最小化乘法次数，
    • 旅行商问题 (TSP)：C(S,j) 为通过集合 S 以 j 结尾的最短路径，复杂度 O(n^2 2^n)。
    • 树上的独立集：最大独立集大小

LIS（最长递增子序列）

1
2
3
4
5
6
7
8
9
Input: 序列 a[1..n]  
Output: LIS 长度  

1. for j = 1 to n:  
2.   L[j] = 1  # 初始化以 j 结尾的 LIS 长度  
3.   for i = 1 to j-1:  
4.     if a[i] < a[j]:  
5.       L[j] = max(L[j], L[i] + 1)  
6. return max(L)

running time: O(n^2)

LCS(最长公共子序列)

1
2
3
4
5
6
7
8
9
10
11
Input: 序列 a[1..n], b[1..m]
Output: LCS 长度
1. for i = 0 to n: L[i,0] = 0  # 初始化第一行
2. for j = 0 to m: L[0,j] = 0  # 初始化第一列
3. for i = 1 to n:
4.   for j = 1 to m:
5.     if a[i] == b[j]:
6.       L[i,j] = L[i-1,j-1] + 1  # 匹配时长度加1
7.     else:
8.       L[i,j] = max(L[i-1,j], L[i,j-1])  # 不匹配时取最大
9. return L[n,m]  # 返回 LCS 长度

running time: O(n*m)

01背包问题

1
2
3
4
5
6
7
8
9
10
11
Input: 物品重量 w[1..n], 价值 v[1..n], 容量 W  
Output: 最大价值  

1. for w = 0 to W: K[w,0] = 0  
2. for j = 1 to n:  
3.   for w = 1 to W:  
4.     if w_j > w:  
5.       K[w,j] = K[w,j-1]  
6.     else:  
7.       K[w,j] = max(K[w-w_j,j-1] + v_j, K[w,j-1])  
8. return K[W,n]

Linear Programming

MAX Flow

1
2
3
4
5
6
7
8
9
10
11
FORD-FULKERSON(G, s, t):
    for each edge (u,v) in G:
        f(u,v) = 0  // 初始化流量
    while exists path p from s to t in residual graph G_f:
        c_f(p) = min{ c_f(u,v) | (u,v) in p }  // 路径剩余容量
        for each edge (u,v) in p:
            if (u,v) is forward edge:
                f(u,v) += c_f(p)
            else:  // (v,u)是反向边
                f(v,u) -= c_f(p)  // 减少正向流量
    return f  // 最大流

Ford-Fulkerson思想：

  • 构建残差图：正向边剩余容量 = c_e - f_e，反向边容量 = f_e
  • 迭代寻找增广路径：在残差图中用BFS/DFS找s→t路径
  • 更新流量：增加路径上最小残差容量的流量
  • 复杂度：O(|V|·|E|²)

Max Flow-Min Cut 定理：最大流等于最小割，即在流网络中，源点到汇点的最大流量等于将网络分割成两部分时，割边的最小容量。

二分图匹配可以通过归约到最大流算法解决，将二分图转化为流网络，源点连接到左侧节点，右侧节点连接到汇点，边的容量为1。

Simplex

Dual LP

Dual LP

P vs NP

P类问题：

  • 存在多项式时间算法可以求解的决策问题
  • 时间复杂度为 O(n^k)，其中 k 是常数

NP类问题：

  • 给定一个解，可以在多项式时间内验证其正确性的决策问题
  • Nondeterministic Polynomial time

NP-Complete问题：

  • 属于 NP 类的问题
  • NP 类中的任何问题都可以在多项式时间内规约到它
  • 如果任何一个 NP-Complete 问题有多项式时间算法，则 P = NP

NP-Complete

Search Problem: 给定实例 I 和解验证器 C(I,S)（多项式时间验证），寻找解 S

搜索问题等价于NP问题。

问题描述对比的 P 类问题
3SAT三变量子句的可满足性2SAT（二变量子句）
TSP旅行商问题（最小代价环游）最小生成树
LONGEST PATH图中最长简单路径最短路径
3D MATCHING三集合匹配（男-女-宠物）二分图匹配
KNAPSACK背包问题（整数权重/价值）单位权重背包（动态规划）
INDEPENDENT SET图中独立集（无相连顶点）树上的独立集
ILP整数线性规划线性规划（单纯形法）

Reductions

A -> B （A不比B更难， A <= B）
Reduction
要点：

  • 实例转换
  • 解转换（无解传递）
  • 均在多项式时间内完成

对于非搜索问题，只需要进行实例转换。

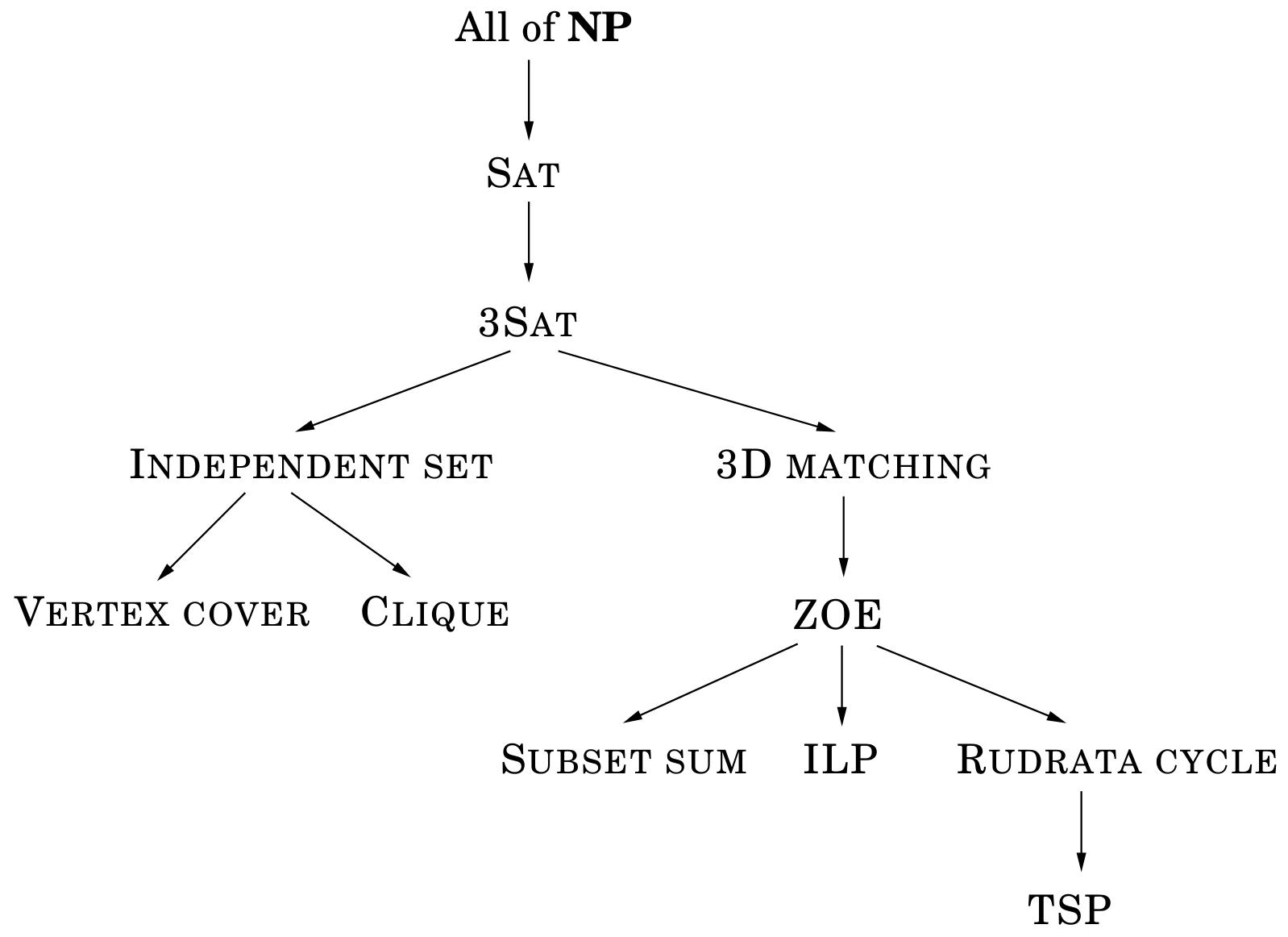
规约链分析：3SAT → INDEPENDENT SET → VERTEX COVER → CLIQUE

1. 3SAT → INDEPENDENT SET（独立集）

  • 目标：将布尔可满足性问题（3SAT）规约到独立集问题。

  • 步骤：
    a. 实例转换：

    • 对包含 k 个子句的 3SAT 公式，构造图 G：
      • 每个子句对应一个三角形（3 个顶点），顶点表示子句中的文字（如 ）。
      • 添加冲突边：若文字互补（如 x 和 ），则在所有三角形间连接它们。
    • 设独立集目标大小 g = k（子句数）。
      示例：公式
      → 两个三角形：

    b. 解转换：

    • 若存在大小为 g 的独立集，则每个三角形选且仅选一个顶点（无冲突边保证不选互补文字）。
    • 令所选文字为 true（如选 x 则 x=true；选 则 x=false
  • 核心洞察：
    独立集选点 = 为每个子句选一个 true 文字，且全局赋值一致。

2. INDEPENDENT SET → VERTEX COVER（顶点覆盖）

  • 目标：将独立集规约到顶点覆盖问题。

  • 步骤：
    a. 实例转换：

    • 给定图 G=(V,E) 和独立集目标 g，直接使用同一图 G
    • 设顶点覆盖目标 b = |V| - g（如 |V|=5, g=2 → b=3

    b. 解转换：

    • 若存在大小 b 的顶点覆盖 C，则 是大小为 g 的独立集。
      （因为 C 覆盖所有边 → 内无边）
    • 若存在大小 g 的独立集 S，则 是大小为 b 的顶点覆盖。
  • 核心洞察：
    独立集与顶点覆盖是互补问题：

3. VERTEX COVER → CLIQUE（团）

  • 目标：将顶点覆盖规约到团问题。

  • 步骤：
    a. 实例转换：

    • 给定图 G=(V,E) 和顶点覆盖目标 b，构造其补图
    • 设团目标 g = |V| - b（如 |V|=4, b=1 → g=3

    b. 解转换：

    • 若 存在大小为 g 的团 K，则 是 G 的大小为 b 的顶点覆盖。
      （因 K 在 中是完全图 → 在 G 中无边 → 覆盖 G所有边）
    • 若 G 存在大小 b 的顶点覆盖 C，则 是 的大小为 g 的团。

    c. 无解传递：

    • 若 无大小为 g 的团，则 G 无大小为 b 的顶点覆盖。

  • 核心洞察：
    顶点覆盖的补集是补图中的团：

alt text
alt text

Other Algorithms

Euclid’s Algorithm

1
2
3
4
5
6
7
8
9
10
11
12
Euclid(a, b) 
// Input: two integers a and b with a ≥b ≥0
// Output: gcd(a, b)
1. if b = 0 then return a
2. return Euclid(b, a mod b)

extended-Euclid (a, b) 
// Input: two integers a and b with a ≥b ≥0
// Output: gcd(a, b) and integers x and y such that ax + by = gcd(a, b)
1. if b = 0 then return (a, 1, 0)
2. (g, x1, y1) = extended-Euclid(b, a mod b)
3. return (g, y1, x1 - (a / b) * y1)

For any positive integers a and b ,the extended Euclid algorithm returns integers x , y ,and d such that go

RSA

1
2
3
4
5
6
7
8
9
10
11
12
1. 随机选择大素数 p, q → 计算 N = p * q
2. 选 e 满足 gcd(e, (p-1)(q-1)) = 1 （互素）
3. 计算 d = e⁻¹ mod (p-1)(q-1)  // 扩展欧几里得（ed ≡ 1 mod φ(n)）
4. 公钥 = (N, e), 私钥 = d

RSA(n, e, m)
// Input: n = p * q, e, m（明文）
// Output: c = m^e mod n

RSA-decrypt(n, d, c)
// Input: n = p * q, d, c
// Output: m = c^d mod n

RSA的正确性基于欧拉定理：

如果 gcd(m, n) = 1，则 m^φ(n) ≡ 1 (mod n)

Prime Testing

费马小定理： 如果 p 是素数且 a 是任意整数，则 a^(p-1) ≡ 1 (mod p)

1
2
3
4
5
6
7
primality2(N) 
// Input: positive integer N 
// Output: yes/no 
1. Pick positive integers a1, a2, ..., ak<N at random 
2. if ai^{N-1} ≡ 1 (mod N ) for all i=1,2, ..., k 
then return yes 
3. else return no.

Pr(primality2 returns yes when N is prime) = 1

Pr(primality2 returns yes when N is not prime) ≤ 1 / 2^k